平成20年度春季解答

問題1

16 ビットの2進数 n を 16 進数の各けたに分けて，下位のけたから順にスタックに格納するために，次の手順を4回繰り返す。a，b に入る適切な語句の組合せはどれか。ここで，xxxx16 は 16 進数 xxxx を表す。

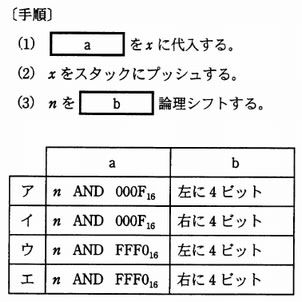
解答：イ

＜解説＞

1. 【　a　】は、下位4ビットを取り出す処理である。下位4ビットを取り出す為には、n に 000F₁₆をマスクする必要がある。
   
2. ｘをスタックにプッシュする。
3. nを右に4ビット論理シフトする。最下位の4ビットのビットパターンが除かれて次の桁の4ビットの取り出しの準備できる。
   

問題へ

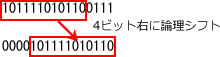
問題2

10 進数の分数	1	を 16 進数の小数で表したものはどれか。
	32

ア	0.01
イ	0.02
ウ	0.05
エ	0.08

解答：エ

＜解説＞

1	＝	8	×	1	×	1
32				16		16
	＝	8	×	1
				162
	＝	(0.08)16

【 別解 】

1	を2進数に変換する
32

0	．	0		0		0		0		1
1		1		1		1		1		1
1		2		4		8		16		32

0.000010000を16進数に変換すると、0.08になる。

問題へ

問題3

負数を2の補数で表すとき，すべてのビットが1である ｎビットの2進数"1111…11" が表す数値又はその数式はどれか。

ア	－（2n-1 - 1）
イ	－1
ウ	0
エ	2n - 1

解答：イ

＜解説＞

1. 2進数"1111…11"のビットを反転する
   →"0000...00"となる。
2. １を加算する
   →"0000...01"となる。
3. 2の補数表現で左端ビットが1なら負数である。
   →-1となる。
   

問題へ

問題4

数値を2進数で表すレジスタがある。このレジスタに格納されている正の整数ｘを 10 倍する操作はどれか。ここで，シフトによるけたあふれは，起こらないものとする。

ア	xを2ビット左にシフトした値にxを加算し，更に1ビット左にシフトする。
イ	xを2ビット左にシフトした値にxを加算し，更に2ビット左にシフトする。
ウ	xを3ビット左にシフトした値と，xを2ビット左にシフトした値を加算する。
エ	xを3ビット左にシフトした値にxを加算し，更に1ビット左にシフトする。

解答：ア

＜解説＞

nビット左にシフトすると、値は2ⁿ倍になる。

ア	○	(22+1)×21=10
イ	×	(22+1)×22=20
ウ	×	23+22=12
エ	×	(23+1)×21=18

問題へ

問題5

浮動小数点表示の仮数部が 23 ビットであるコンピュータで計算した場合、情報落ちが発生する計算式はどれか。ここで、( )₂内の数は2進法で表示されている。

ア	(10.101)2 × 2-16 - (1.001)2 × 2-15
イ	(10.101)2 × 216 - (1.001)2 × 216
ウ	(1.01)2 × 218 + (1.01)2 × 2-5
エ	(1.001)2 × 220 - (1.1111)2 × 221

解答：ウ

＜解説＞

情報落ちとは、大きな値と小さな値を加減算したときに、小さな値が無視されてしまう現象のことである。 仮数部のビット数が23ビットなので、情報落ちが発生するのは、加減算する数値の絶対値の差が2²³以上あるときです。この条件を満たすのはウだけである。よって正解はウである。

問題へ